Introduction
I was reading the news the other day when I stumbled upon an article about exoplanets — planets that are not in our solar system. The article referenced this web page that provided a Figure of Merit (FOM) for the similarity of an exoplanet to Earth. I am going to examine this FOM to determine what I can learn about it.
The subject of exoplanets has become pretty interesting in recent years. When I was a boy, all the scientific articles at the time described the search for exoplanets as hopeless. Today, scientists regularly find exoplanets by detecting the wobble planets induced in a star or the dimming of a star when a planet passes in front of it. Isn’t it strange how something can go from impossible to commonplace in one generation?
I like this web page because it actually includes data that we can perform mathematical experiments on. This allows me to check my knowledge — if I can compute their results using their data then I probably understand what they are doing.
Background
Once a scientist has detected an exoplanet, one of the first questions is — could it support life? But what does it mean for a planet to support life? We know the Earth supports life, so if the exoplanet is physically similar to Earth then it might also support life. This is where the FOM comes into play.
FOMs are used all the time in engineering. They allow us to rank implementations relative to things like cost, performance, portability and any other criteria we deem important. In the case of an exoplanet, this web page defines the following criteria as important for habitability:
- radius
Exoplanets have a wide range of sizes. Even in our own solar system, the Earth is small relative to the Jupiter and Saturn. There is some evidence that planets need to be near Earth-size to form a liquid core and magnetic field.
- density
The Earth is considered a rocky planet. A planet similar to the Earth should have a similar density.
- surface temperature
Earth-like biology lives in a very narrow temperature range. Because temperature is so important, this criterion should be weighted higher than the others.
- escape velocity
Escape velocity is related to the acceleration due to gravity.
You could easily come up with other parameters to use for our planet habitability FOM. Obvious things are:
- presence of water
- presence of oxygen
- presence of an atmosphere
The problem is that these characteristics are not easily measurable. The FOM discussed here can be computed using readily available parameters. The FOM can then be used to identify the exoplanets that should have priority for further evaluation.
Analysis
FOM Definition
Equation 1 shows the Earth Similarity Index (ESI) used by the Planet Habitability Lab of the University of Puerto Rico.
| Eq. 1 |
where
- xi is the value of the ith planetary parameter (e.g. surface temperature)
- xi0 is the value of the ith planetary parameter for Earth (our reference)
- wi is the weighting exponent assigned to the ith planetary parameter (arbitrary value indicating relative value)
- n is the number of planetary parameters
Equation 1 is used to define three ESI FOMs:
- Interior ESI
This ESI is based on the exoplanet’s radius (weight exponent = 0.57) and density (weight exponent = 1.07).
- Surface ESI
This ESI is based on the exoplanet’s surface temperature (weight exponent = 5.58) and escape velocity (weight exponent = 0.70).
- Global ESI
A composite of both the interior and exterior ESI’s.
I will demonstrate how to compute the values of these ESI’s using Mathcad.
Equation 1 is interesting because the weighting factors show the relative priorities that the astronomers assign to the planetary parameters. For example, surface temperature is given a very high weight, while the radius of the planet is given much less weight. This makes sense because the biochemical reactions that we know of can exist in only a narrow temperature range.
What do astronomers know about the exoplanets they discover?
I am not an astronomer, so I am inferring this information from my reading. Astronomers appear to get reasonably accurate values for the following planetary characteristics:
- Revolution period around the star
This measurement is fairly accurate when planets are detected by the wobble method.
- Mass
Bigger planets make bigger wobbles. Astronomers will have good information on the mass of the star that the exoplanet orbits. This should allow them to obtain good mass estimates.
- Planet Radius
This measurement can be made using the transit method. The bigger the planet, the more the star’s light is obstructed.
- Orbit Eccentricity
The wobble characteristics should be able to give you this information.
- Albedo
See this web page for a discussion of how astronomers can get an indirect measurement of albedo. The albedo measurement is important for getting a good estimate of the exoplanet’s temperature.
Applying a bit of celestial mechanics can then give you the following information:
- Orbit Radius
Knowing the period of revolution, Kepler’s law will give you the major axis distance of the planet’s orbit.
- Density
Straightforward calculation given planetary mass and radius.
- Surface Gravity
See the gravitational acceleration article on the Wikipedia.
- Escape Velocity
See the escape velocity article on the Wikipedia.
- Surface Temperature
See the effective temperature article on the Wikipedia. I cannot do a better job explaining the concept than they did. Note that determining the surface temperature requires knowing information about the albedo of the planet. Albedo data was not given on this web site, so I will not attempt to compute the surface temperature.
Figure 1 shows the equations that I did use to compute orbit radius, density, escape velocity, and surface gravity.
Appendix A contains a PDF file that shows the formulas of Figure 1 being used to compute the information required for the ESI calculation. As expected, I obtained the same results as the web page.
Calculation Method
I thought I would try to recompute their ESI results for the bodies in our solar system, which the web page authors also did. This means that I can compare my results to theirs. To keep my calculations simple, I only kept the data for bodies that rotate about the Sun, which allowed me to only have to deal with one value for Kepler’s constant. The method of calculation would be identical for bodies that do not rotate around the Sun, but Kepler’s constant would be different because the rotation is not about the Sun.
I downloaded their data files into Mathcad and computed the ESI using the Mathcad program shown in Figure 2.
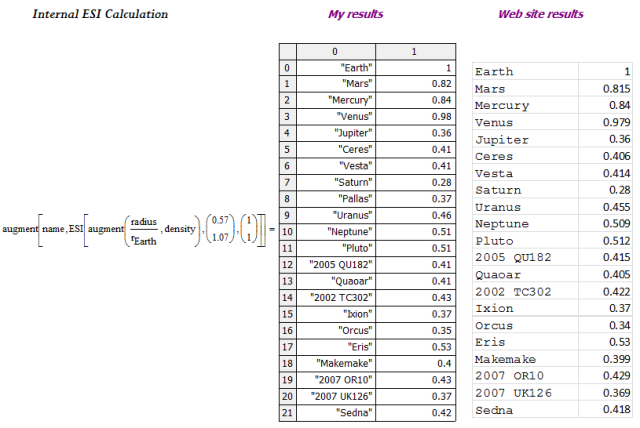
Internal ESI Calculation
Figure 3 shows my calculation for the internal ESI value.
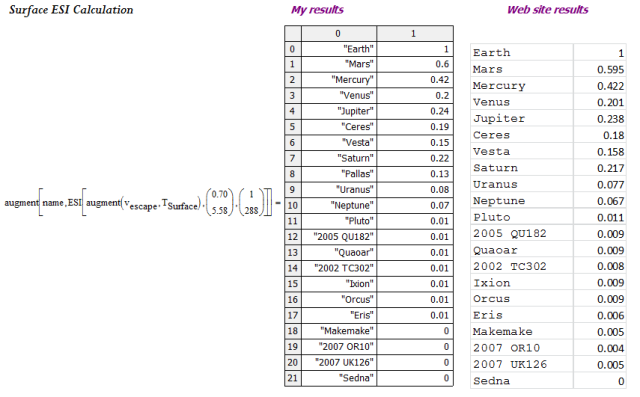
Surface ESI Calculation
Figure 4 shows my calculation for the surface ESI value.
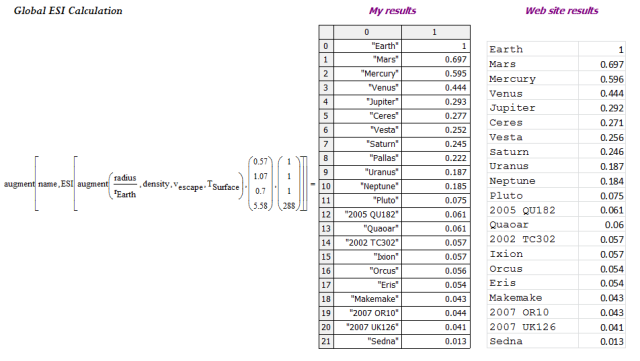
Global ESI Calculation
Figure 5 shows my calculation for the global ESI value.
Conclusion
I was able to reconstruct the original web page results for the ESI of the various bodies in our solar system using their data plus simple celestial mechanics. This sort of calculation might be interesting for a high-school or early college science student.
Appendix A: PDF Version of My Calculations
People often ask me for copies of my original work. Since Mathcad is not as common as it should be, I will first include a PDF version of my work here.
PDF Version of My Mathcad Work
Here is a link to the raw Mathcad 15 file. It is an XML file — just save it to your disk and run Mathcad on it.




Pingback: Calculating the Number of Observable Life-Supporting Planets | Math Encounters Blog